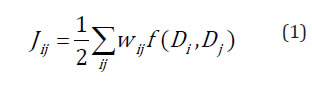
ORIGINAL ARTICLE
Spatio - temporal spread of Plum pox virus infecting European plum (Prunus domestica L. cv. D'agen) orchard in Mendoza, Argentina
Distribución espacial y temporal del Plum pox virus en un monte de ciruelo europeo (Prunus domestica L. cv D'agen) de Mendoza, Argentina
Angélica Dal Zotto 1*, Laura B. Porcel 2, Diana B. Marini 3, Cecilia N. Picca 2, Mariano Córdoba 4, Ingrid Teich 5
1 Instituto de Patología Vegetal. CIAP-INTA. Av. 11 de Setiembre 4755. C. P. X5020 ICA- Córdoba. Argentina. * dalzotto.angelica@inta.gov.ar
2 Estación Experimental Agropecuaria Rama Caída. INTA. El vivero s/n. C. P. 5600. San Rafael. Mendoza. Argentina.
3 Estación Experimental Agropecuaria Junín. INTA. Carril Isidoro Busquets. La Colonia. C. P. 5573. Junín. Mendoza. Argentina.
4 Universidad Nacional de Córdoba. Facultad de Ciencias Agropecuarias. Cátedra de Estadística y Biometría. CONICET. Av. Valparaíso s/n. C. P. 5000. Córdoba. Argentina.
5 Instituto de Fisiología y Recursos genéticos vegetales (CIAP)-INTA. CONICET. 11 de Setiembre 4755. C. P. X5020 ICA. Córdoba. Argentina.
Originales: Recepción: 20/09/2016 - Aceptación: 12/03/2019
ABSTRACT
Sharka, caused by Plum pox virus (PPV), is considered one of the most serious viral diseases of stone fruits worldwide due to the great yield losses in orchards. In Rama Caída, Mendoza, a 5-year study (2007-2011) was conducted in a European plum cv D’agen orchard using samples from leaves and DAS-ELISA assay against PPV in order to determine incidence over time and spatial spread. Incidence significantly increased between 2007 and 2009, while for the next two years the increase was not statistically significant. Spatial point pattern of PPV at the plot was characterized by the occurrence of some heterogeneous clusters of infected trees located up to 65 m in the west-east direction of the rows over the five years. Point pattern and correlation type-approaches were undertaken using joint-count and Ripley's K function and showed that the detected infected plants had a disease aggregation pattern both in west-east and south-north directions, as well as within and between rows across the plot. This short-distance local dispersion would be associated with diverse factors, such as vector aphids, that were not evaluated in this study. Hence, this work can serve as a basis for further studies of sharka dispersion in Cuyo region.
Keywords: Sharka; Prunus domestica cv. D'agen; Temporal and spatial virus statistical analysis; PPV
RESUMEN
Sharka causada por Plum pox virus (PPV) es considerada la enfermedad más nociva de los frutales de carozo debido a las pérdidas que produce en los montes frutales. En Rama Caída (Mendoza) se estudió la dispersión del PPV en un monte de ciruelo europeo cv D’agen durante 2007 a 2011 a través del análisis de muestras de hojas de árboles individuales por DAS-ELISA, para determinar la incidencia y distribución espacial de virus. Entre 2007 y 2009, el aumento en la incidencia fue estadísticamente significativo mientras que en 2010 y 2011 este no resultó significativo. El PPV se distribuyó en el lote, como un patrón de puntos caracterizado por agrupamientos heterogéneos de árboles infectados, ubicados hasta los 65 m en dirección oeste-este de las filas. A través del análisis de patrones de puntos y de correlación de árboles infectados, mediante la función K de Ripley y el estadístico Joint-count, se comprobó que las plantas infectadas presentaron un patrón espacial agregado, tanto en sentido oeste-este (entre filas), como sur-norte (dentro de fila), indicando una dispersión a corta distancia. Este escenario puede responder a múltiples factores no estudiados, como la presencia de áfidos vectores, y constituir las bases de futuros estudios de dispersión de PPV en Cuyo.
Palabras clave: Sharka; Prunus domestica cv. D'agen; Análisis estadístico espacial y temporal del virus; PPV
INTRODUCTION
Sharka disease, caused by Plum pox virus (PPV, genus Potyvirus, family Potyviridae) is considered one of the most destructive diseases of stone fruit (apricots, Japanese and European plum, peach and cherry) worldwide (8, 15).
The disease causes important economic losses in stone fruit orchards affecting the appearance, flavour and texture of fruits, to the point of making them undesirable both for fresh consumption and industry. It may also cause premature fruit drop, thereby reducing production (15).
The virus was first detected in Bulgaria (1) and is present in countries of Western and Eastern Europe, Northern Africa and North and South America. In Argentina, it was detected in 2004 (12) in Japanese plum and apricot orchards in San Juan province and, more recently, in European plum in Mendoza province. PPV is disseminated via infected propagation material (buds, grafts) from one place to another, such as between countries, and/ or regions/locations within a country. Deficient or absent sanitary control between regions is considered the cause of PPV introduction to virus-free areas (2).
Once PPV is introduced to a geographical site, local dissemination among nearby plants can occur through vector aphids. There are about 20 aphid species that can transmit the virus in an uncontrolled, natural manner, carrying the virus from a diseased plant to healthy ones (23). There is no direct correlation between virus transmission capacity and vector Prunus colonization, because PPV can be efficiently transmitted both by species that do not colonize stone fruit trees (visitor aphids) and by species that form colonies in Prunus, with leaves and fruits being the main inoculum sources (24). While the disease expands rapidly in fruit orchards, progression rate can vary with the PPV strain (D or M, or others such as REC) and the Prunus species involved (plum, apricot or peach)(17, 24).
Studies on PPV dispersion in stone fruit trees have been conducted in different European countries over several years, such as Spain (18) France (11) and Greece (33), as well as USA and Canada in North America (20) involving different Prunus species. Their results showed that the spatial dispersion of PPV responds to different distribution patterns (8, 11, 18, 20, 24, 33). Data collected by intensive mapping include details of the spatial arrangement of sampling units.
The disease distribution pattern is a characteristic that can be attributed to a series of points (infected trees) and that describes their location in terms of relative distance of each point with respect to the remaining ones (32). Given that plant disease data can display spatial patterning in a number of different ways, it is useful to analyze spatial patterns using different approaches and search for congruence in the detected patterns (14, 28).
Accordingly, Join-count statistics (10) may be used to analyze spatial association for disease incidence data (26). This approach is appropriate when each individual plant is considered a sampling unit. Another robust method to measure the randomness of binary data of spatial points are the stochastic models proposed by Ripley (14, 30) widely used for analysis of spatial patterns, both in local dispersion (i.e. within row and across rows) (31) and regional dispersion (long distance dispersion) (19, 20).
Models are also used to understand how plant diseases develop in a population over time. With models, the many individual observations are reduced to a few model terms, making it much easier to visualize and, ultimately, understand the studied phenomena (26).
Generalized linear mixed models (GLMMs) are an appropriate tool for evaluating virus incidence over time based on binary variables allowing taking into account possible correlations between observations measured on a single individual over time (25).
According to this, we postulate that a point pattern of infected PPV trees on orchards has an aggregated or clustered spread. A random distribution (complete spatial randomness, CRS) would be the null hypothesis for statistical analyses, whereas the alternative hypothesis postulates that the distribution pattern of infected trees is either regular or clustered (27). The aim of this work was to analyze and evaluate the spatial and temporal natural spread of Sharka virus in an European plum orchard in the southern area of Mendoza province, Argentina, from 2007 to 2011.
MATERIALS AND METHODS
Orchard sampling design
The study was conducted in a European plum (Prunus domestica L. cv D'Agen) orchard located in Rama Caída district (34° S, 68° W), San Rafael department, southern Mendoza province, Argentina. The orchard (1 ha) is characterized by a rectangular planting pattern of 3 x 4 m spacing between plant and row, comprising 750 trees on 25 rows (100 m) in west-east direction and 90 m in south-north direction. Sampling was performed during spring (October) from 2007 to 2011, and included all the trees in the orchard, some of which exhibited chlorotic symptoms and ring spots in leaves, as well as premature fruit drop.
Virus detection
Samples of expanded leaves (16 leaves per plant) were taken from branches oriented to the four cardinal points. The double antibody sandwich-enzymelinked immune sorbent assay (DAS- ELISA) was used, following the protocol of Clark and Adams (1977), using Inmunoglobulins and conjugates of PPV (Bioreba). Plates (NUNC 96-well polystyrene) were coated using 1:1000 IgG dilutions and conjugate. The extract was processed using 0.5 g of basal third of leaves diluted in 1/10 w/v extraction buffer.
Commercial positive controls (Bioreba) and negative controls (virusfree plum or healthy controls) were used. Plates were read at 405 nm in a Bio-TEK ELX800 Reader. Plants were considered healthy when their absorbance reading value was higher than twice the mean of healthy control plants.
Temporal analyses
Virus incidence and dispersion for the whole plot (750 trees) was assessed from 2007 to 2011. PPV infection was confirmed by DAS-ELISA, resulting in diseased trees (classified as D) and non-infected-healthy trees (classified as H). With these values of disease status, the incidence progress curve was fitted for the evaluated period with a generalized linear mixed model (GLMM) with the logit link function (25).
Year was included as a fixed effect and tree as a random effect in order to account for the intra-tree correlation along the years.
The estimated mean annual disease incidence was compared between years using the a posteriori test of Fisher's LSD (α=0.05). Analyses were performed using the software InfoStat (13).
Spatial analyses
Spatial distribution of PPV in Rama Caída orchard was analyzed via a spatial autocorrelation analysis, showing the spatial effects using georeferenced data, here applied at an individual tree level. We used two analyses in order to study the spatial pattern of PPV disease: 1) join-count statistics (10), and 2) Ripley's K function (30). Both methods describe the degree of clustering of individuals, in this case, in relation to PPV presence. The values of these statistics indicate if the pattern is clustered, random or dispersed.
Join-count
Join-count statistics is an area pattern method used to assess the spatial association of categories. We considered two point classes, D and H, where D represents virus presence in trees and H, absence of the disease in the tree, to determine the number of pairs of points with the same characteristic (presence or absence, DD or HH), within a neighbourhood defined by the distance between trees. Then the method calculates if the number of pairs of the same type, e.g., DD (i.e., both trees are infected) is higher or lower than the value expected by chance, considering the total number of Ds and Hs and the number of pairs of points defining the neighbourhood.
A similar approach is used for the events in which the pairs of HH trees (healthy plants) or DH trees (one healthy and one infected plant) are counted.
The neighbourhood was represented by a connectivity matrix (W) of N×N in size, where N is the number of trees and each W element (wij) has a value of 1 to 0, depending on whether the ith tree is neighbour of the jth tree (wij =1) or not (wij =0). For example, in cases of points of the same type (DD) the statistic Jij is defined as equation (1):
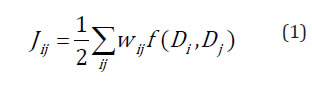
where:
f(Di, Dj) is a function of a value of 1 if trees i and j are D type, and of 0 (f(Ai, Aj)=0) if any of the trees i and j are not type D, for all i≠j.
The indices considering the number of adjacent (neighbours) Joins of the same type (DD or HH) quantify the degree of positive spatial autocorrelation, whereas the index based on the number of adjacent regions that do not contain the same category (DH) describes the degree of negative autocorrelation. We defined neighbours using a distance-based connectivity matrix W, where neighbours were defined as locations within 4 m, from 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64 up to 100 meters, which corresponds to the entire west-east length of the plot. The results are expressed for each pair of connections (DD, HH, DH) as a standard normal deviate (SND), obtained by subtracting the expected paired values from the observed ones and dividing by the standard deviation. Thus, significance (α = 0.05) of SND would correspond to a ±1.96 threshold. To confirm the null hypothesis, a permutation procedure was used via Monte Carlo simulation, by which the categories are randomly reassigned with each simulation and the "join count" statistic of interest is calculated.
The fraction of simulations with a statistical value below the observed one, provides the p value. We used join count statistics to address whether the observed DD was considerably larger than expected in each evaluated year. The join-count statistic was calculated using the spdep library (6) in R (29).
Ripley’s K function
The spatial concentration of points in the absence of randomness determines the interaction or spatial dependency among points across space, which is also described with the Ripley’s K function. If “y” is the mean of infected trees per unit area (density), then yK(d) is the number of infected trees within the distance (d) from an arbitrarily selected infected tree.
If a group of points is randomly distributed, for example via a Poisson process with λ density, the expected number of points in a circle of "d" radius is λπd2; thus, the Ripley's K function (30) can quantify the deviation from randomness (theoretical distribution) and reflect the type, intensity and range of the spatial pattern by analyzing the distances between all points. In this study, which is based on a rectangular plot, the equation (2) is fitted:
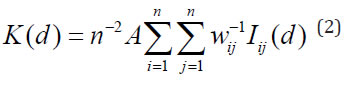
for i≠ j
where:
n = the number of points (trees) in the sample
A = the plot area in m2
wij = the correction factor of the edge effect
Iij (d) equals 1 if dij ≤d and 0 if dij>d, with dij being the distance between points i and j.
The factor wij is calculated
following (16). The function L (modified
Ripley’s K function) ![]() was
used to linearize the function and stabilize
the variance. This implied representation of L (d)-d against distance d, thereby
fitting the null hypothesis to a value of
zero (4).
was
used to linearize the function and stabilize
the variance. This implied representation of L (d)-d against distance d, thereby
fitting the null hypothesis to a value of
zero (4).
Therefore, an aggregate pattern occurs when L(d)-d is significantly higher than zero and a regular pattern, when L(d)-d is significantly lower than zero (31). The null hypothesis of spatial randomness was proven via 100 Monte Carlo simulations. To ensure the performance of a significance Monte Carlo test at 0.05 level, 999 simulations were performed (5, 7). Ripley's K function was modelled using the spatstat library (3) in R (29).
RESULTS
Temporal disease progression
The results of the DAS-ELISA analysis, showed 19 positive trees in 2007, 15 new infected plants in 2008 and 14 new infected plants in 2009, whereas in 2010 and 2011, only 6 and 10 new plants were infected, respectively (table 1).
Table 1. Analysis of European plum cv D'agen for Plum pox virus by DAS- ELISA in a plot from Rama Caída, Mendoza, Argentina.
Tabla 1. Análisis por DAS-ELISA de Plum pox virus en ciruelo europeo cv D'agen en un monte de Rama Caída, Mendoza, Argentina.

The initial incidence was 2.53% in 2007, then 2% in 2008, 1.86% in 2009, 0.8% in 2010 and 1.34% in (2011), respectively. A total of 64 new plants infected with PPV were detected over the five years (table 1).
The fitted generalized linear mixed model (GLMM) showed significant increases in incidence between 2007 and 2008 and between 2008 and 2009 whereas in the last two years (2009-2011), the increase in incidence was not statistically significant.
The proportion of infected trees over time was 2.5 % (± 0.6) in 2007; 4.5% (± 0.8) in 2008, 6.4 % (± 0.9) in 2009; 7.2 % (± 0.9) in 2010 and 8.5 % (± 1.0) in 2011.
The disease cumulative incidence increased over time. However, between 2009 and 2011, the rate of increase was lower than at the beginning of the study, as shown by the disease progress curve (DPC) (figure 1, page 267).
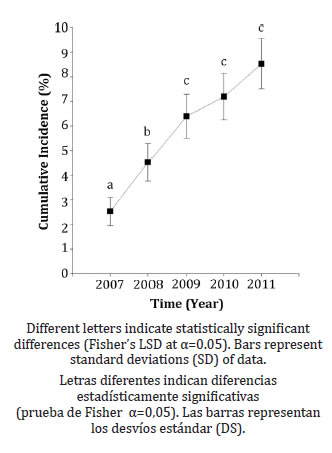
Figure 1. Disease progression curve (DPC) of sharka disease (Plum pox virus infection) in a plot of European plum cv D'agen in Rama Caída, Mendoza, during 2007-2011. The figure shows the cumulative incidence of PPV over the 5-year study period.
Figura 1. Curva de progreso de la enfermedad de sharka (DPC) (Plum pox virus) en un monte de ciruelo europeo cv D' agen de Rama Caída (Mendoza) estudiado entre 2007 y 2011. Se muestra la incidencia acumulada (%) en cada año.
Spatio-temporal point pattern analysis The spatial distribution pattern of PPV infection in the European plum cv D'agen orchard showed that diseased trees were not randomly distributed. Rather, the pattern found was "heterogeneous aggregation" of infected plants within the plot.
The distribution map of infected trees and healthy trees of the studied orchard is represented in a scatter plot (figure 2, page 268-270), with each point representing a tree.
Figure 2. Spatial and temporal analysis of Plum pox virus (PPV) infection in a plot of European plum D’agen during 5 years (2007-2011).
Figura 2. Análisis de la distribución espacial y temporal del Plum pox virus (PPV) en un lote de ciruelo europeo durante 5 años (2007-2011).
Figure 2 (cont.). Spatial and temporal analysis of Plum pox virus (PPV) infection in a plot of European plum D’agen during 5 years (2007-2011).
Figura 2 (cont.). Análisis de la distribución espacial y temporal del Plum pox virus (PPV) en un lote de ciruelo europeo durante 5 años (2007-2011).
Figure 2 (cont.). Spatial and temporal analysis of Plum pox virus (PPV) infection in a plot of European plum D’agen during 5 years (2007-2011).
Figura 2 (cont.). Análisis de la distribución espacial y temporal del Plum pox virus (PPV) en un lote de ciruelo europeo durante 5 años (2007-2011).
At the beginning of the study (2007), the disease was located in the first five rows of plants (up to 20 m), with west-east direction in the plot (figure 2A, page 268).
In the second year (2008), new diseased trees were observed around the initially infected trees, forming heterogeneous associations, which did not extend more than 20 m (figure 2B, page 268), and another group of isolated plants was observed at between 45 and 65 m during the third year (2009) (figure 2C, page 269), New plants in the clustered group around the trees detected in the first years were detected in the last study year (2011), as well as other isolated plants or weakly clustered plants, which appeared at a distance of 70 to 100 m (figure 2D, page 269; figure 2E page 270; table 1, page 266).
Evaluation of the spatial point pattern by join-count method
The results obtained using the joincount statistic showing the joins of the same type category (DD), and adjacent (neighbours) to the presence-presence (DD) infection class, are presented in table 2 (page 271).
Table 2. Spatial analysis of Plum pox virus dispersion in a European plum cv D'agen plot using the join-count autocorrelation statistic.
Tabla 2. Análisis espacial de la dispersión del Plum pox virus en un lote de ciruelo europeo cv D'agen a través del estadístico de autocorrelación Join-count.
They reject the null hypothesis of a random distribution of diseased plants (p-value<0.01) and indicate aggregated clustered disease distribution pattern. Autocorrelation was observed between individuals close to a given tree with respect to those located at a distance between 0 and 96 m in east-west direction.
In table 2 (page 271), we present only the DD presence-presence category (join-count statistic data), which was considerably larger than the expected value (value under complete randomness) in the five years evaluated.
The analyses show that the calculated join-count statistic was higher than expected for each year and for each one of the distances considered to define the neighbourhoods for each tree.
For example, in the second study year (2008), the value recorded at 4 m was 4.75 vs 0.75 (expected value), at 8 m (2.93 vs 0.75), showing that this significant difference is large up to 60 m (1.05 vs 0.75), with a statistical significance p-value of 7.9×10-16.
The difference starts decreasing at 64 m and up to 96 m (data not shown), with a join-count of 0.79 at 96 m in 2008, which is close to the expected value (0.75) under randomness, while p-value increases to 4.4×10-16.
The same trend is observed in the following years: 2009 (1.88 vs. 1.51); 2010 (1.84 vs. 1.77) and 2011 (2.63 vs. 2.52).
A reduction of the statistic value is observed with increasing distance, indicating a lower significant difference between the observed and the expected values at 96 m. However, the difference remains significant, indicating aggregation of diseased plants (p value<0.05) and positive autocorrelation between nearby individuals.
Evaluation of the spatial point pattern by Ripley’s K-function method
The analysis of the PPV virus spatial spread via Ripley's K statistic indicated a non-random distribution of diseased trees as well as a clustered pattern in the plot. Ripley’s K function was fitted for each sampling year (2007 to 2011) and data of virus presence in trees were compared as a function of the distance between them.
Figure 2 (page 268-270), shows the graphs of the theoretical Ripley’s function and the fitted function for a maximum distance (r) of 23 m, corresponding to a quarter of the total distance between trees 90 m in south-north direction.
The envelope ∝= 0.05 (Khi (r)-Klo (r)) for the theoretical distribution under Complete Spatial Randomnes, obtained by Monte Carlo simulation, is shown in grey. The empirical function Kobs(r) obtained from the data collected for each year evaluated was above the theoretical function Ktheo(r) and the simulated envelopes, suggesting that trees infected with PPV show a clustered pattern. The separation between the collected Kobs data and the Ktheo theoretical curve was greatest in 2007, decreasing in the following years, even in 2011. Therefore, in the first year there would be a higher spatial dependency in the distribution of infected plants. This distribution is observed along the distance (23 m) analyzed by the Ripley’s K function. Spatial dependency was higher during the first two years of study, when incidence was higher.
DISCUSSION
The European plum plot evaluated for PPV presence in Rama Caída is the only plot where PPV has been detected in San Rafael up to now.
Sample collection was made under controlled management conditions during the study period. After the end of this study, the process of eradication of positive plants, following the regulatory process for diseases of quarantine concern, was implemented.
In the D'agen plum plot, PPV positive trees were serologically detected by DAS-ELISA during the 5-year study period (2007-2011), showing increasing number of diseased plants over time. This finding indicates that the virus dispersed to healthy trees in the plot over time, but with a significantly lower number of infected plants in the last years than in the first two years, suggesting that PPV epidemic was at very early stage during the study.
PPV distribution observed by the spatial and temporal pattern suggests that PPV has spread naturally, forming heterogeneous aggregations of diseased trees in the orchard. The number of infected plants that appeared with increasing distance, gradually decreased from the focus of the earliest infected plants and especially in the last two years of study with respect to the plants detected in the first three years.
In the plum orchard in Rama Caída, spatial clusters were observed at 4 m within the row (from initial focus) and up to 65 m across rows. These small clusters indicated a relationship between sharka diseased trees (D) that were at a close distance. Over time, other isolated or weakly clustered plants appeared at a distance of 70 to 100 m (W-E) in 2010-2011, indicating a lower disease progression over space and time.
Heterogeneous aggregated spatial associations occurred close in space and time, which was confirmed with similar approximation by autocorrelation spatial analysis with Ripley's K function and Join-count. This result supports the hypothesis of tree aggregation and is in agreement with Madden et al. (2007). Our results indicate an aggregated point pattern that has a positive correlation, i.e. between the infected tree and the distance between each one.
The results also suggest that the spatially closest trees had a greater probability of becoming infected than healthy trees separated from diseased ones (at least up to 96 m), which is in agreement with Madden et al. (2007). Accordingly, studies of PPV-D spread in orchards from Pennsylvania (USA), conducted using autocorrelation analyses between 1999 and 2000, reported the presence of clusters, which were stronger within rows than between rows, with fewer and smaller aggregations with increasing distance (17, 20). Similarly, in apricot orchards infected with PPV-D in France, new symptomatic trees were sometimes found to be close to previously infected ones, forming infection clusters over time (24).
Other findings of PPV-D spread reported for orchards in Pennsylvania and Canada indicated that a few clusters of new infected trees appeared around already infected trees, within a range of 25-150 m (17, 20). All of these findings are in agreement with or similar to our results.
By contrast, in eastern Spain, no clusters of trees infected with PPV-D were observed between adjacent trees or within rows in apricot and peach orchards. Rather, the clusters were formed at greater distances and with no specific direction, i.e., no spatial disease gradients were observed over time (18). In Rama Caída orchard, we observed a west-east trend of PPV spread. However, the formation of new associations of positive trees occurring over time did not show a disease gradient in the plot.
Studies on the spatial distribution of PPV-D conducted in different countries attributed the formation of spatial aggregations at a short distance (less than 100 m) to the virus transmission by viruliferous aphids. Distribution can result in aggregations or groups of trees that are both far from the initially infected trees and around the trees immediately adjacent to an infected tree (8, 18).
Our study shows that the area infected with PPV has expanded from west to east, coinciding with the prevailing wind direction in the area. This fact, along with results on the distribution pattern and the short distance evaluated, would suggest that the observed spread might be associated with movement of aphid vectors, a fact that has not been evaluated in this work. It has been suggested that PPV expansion would depend both on the presence of and proximity to viruliferous aphids sources (34).
The fruit species and the cultivar would also contribute to susceptibility to PPV and to the aphid, as observed in Chile (21, 22) and in France (23).
Our future research on sharka disease and PPV spread will focus on vector presence and aphid species disseminating PPV, their population dynamics and virus transmission efficiency.
CONCLUSION
The natural dispersion of Plum pox virus in European plum analyzed and quantified using mixed generalized models and functions with autocorrelation analysis, was led to determine the movement of infection among close spatially plants. These tools allowed to contrast the hypothesis of randomness of the disease in the infected bush, resulting in an aggregate distribution of the disease in aggregate, under the presence of clusters of infected trees. In turn the incidence of the disease was higher at the beginning of the study and lower for the following years, meaning that the infection rate among nearby trees decreased over time as dispersion distance increased from the first test plants. These results allowed us to evaluate the movement of the disease in European plum cv D'agen, which could be used in future studies of distribution of the virus in other cultivars or species of stone fruit and other growing regions in Argentina, as well as to improve disease management and control measures.
1. Atanasovv, D. 1932. Plum pox. A new virus disease. Annals of the University of Sofia. Faculty of Agriculture and Silviculture. 11: 49-70.
2. Auger, J.; Esterio, M. 1995. La enfermedad de la Sharka (Plum pox Virus) en Chile. Revista Aconex. 47: 25-8.
3. Baddeley, A.; Turner, R. 2008. Spatstat: An R package for analyzing spatial point patterns. Journal of Statistical Software. 12 1-42.
4. Besag, J. 1977. Contribution to the discussion of Dr. Ripley’s paper. J R Statist Soc B 39 193-5.
5. Besag, J.; Diggle, P. J. 1977. Simple Monte Carlo tests for spatial pattern. Appl Stat. 26: 327-33.
6. Bivand, R. 2014. Spdep: Spatial dependence: weighting schemes, statistics and models version 0.5-74/r555 http://R-Forge.R-project.org/projects/spdep/
7. Bryan, F.; Manly, J. 1997. Randomization, Bootstrap and Monte Carlo Methods in Biology. London. ed. CH CRC.
8. Cambra, M.; Capote, N.; Cambra, M. A.; Llácer, G.; Botella, P.; Lopez-Quilez, A. 2006. Epidemiolgy of sharka disease in Spain. Bulletin EPPO. 36: 271-5.
9. Clark, M.; Adams, A. N. 1977. Characteristics of the microplate method of enzyme-inmunosorbent assay for the detection of Plant Virus. Journal of General Virology. 34: 475-83.
10. Cliff, A. D.; Ord, J. K. 1981. Spatial Processes: Models and Applications. London. ed. 266 p.
11. Dallot, S.; Gottwald, T.; Labonne, G.; Quiot, J. B. 2003. Spatial pattern analysis of sharka disease, Plum pox virus Strain M, in Peach Orchards of Southern France. Phytopathology. 93: 1543-52.
12. Dal Zotto, A.; Ortego, J. M.; Raigón, J. M.; Callogero S.; Rosssini M.; Ducasse D. A. 2006. First report in Argentina of Plum pox virus causing Sharka disease in Prunus. Plant Disease. 90: 523.
13. Di Rienzo, J. A.; Casanoves, F.; Balzarini, M. G.; Gonzalez, L.; Tablada, M.; Robledo, C. W. 2014. InfoStat version 24-03-2014 Grupo InfoStat. FCA Universidad Nacional de Córdoba Córdoba. Argentina. Available in: http://www.infostat.com.ar/
14. Dixon, P. M. 2002. Ripley's K function En: AH El-Shaaraui, WW Piergorsch (Ed).The encyclopedia of environmetrics. New York. Wiley. 1796-803.
15. García, J. A.; Glasa, M.; Cambra, M.; Candresse, T. 2014. Plum pox virus and sharka: a model potyvirus and a major disease. Molecular Plant Pathology 15: 226-41.
16. Getis, A.; Franklin, J. 1987. Second-order neighborhood analysis of mapped point patterns. Ecology. 68: 473-7.
17. Gottwald, T. 2006. Epidemiology of sharka disease in North America. Bulletin EPPO. 36: 279-86.
18. Gottwald, T.; Avient, L.; Llácer, G.; Hermoso de Mendoza, A.; Cambra, M. 1995. Analysis of the spatial spread of Sharka (Plum pox virus) in apricot and peach orchards in eastern Spain. Plant disease. 79: 266-78.
19. Gottwald, T. R.; Sun, X.; Riley, T. R.; Graham, J. H.; Ferrandino, F.; Taylor, E. 2001. Geo-Referenced spatiotemporal analysis of the urban citrus canker epidemic in Florida. Phytopathology. 92: 361-77.
20. Gottwald, T. R.; Wierenga, E.; Luoa, W.; Parnell, S. 2013. Epidemiology of Plum pox 'D' strain in Canada and the USA. Canadian Journal of Plant Pathology. 35: 442-7.
21. Herrera, G. 2013. Investigations of the Plum pox virus in Chile in the past 20 years. Chilean journal of agricultural research. 73: 60-5.
22. Herrera, G.; Madariaga, M. 2003. Diseminación natural del virus causante de la enfermedad de sharka (Plum pox virus) en tres termporadas en un huerto de damasco. Agricultura técnica. 63.
23. Labbone, G.; Dallot, S. 2006. Epidemiology of sharka disease in France. Bulletin EPPO. 36: 267-70.
24. Labbone, G.; Yvon, M.; Quiot, J. B.; Avinent, L.; Llacer, G. 1995. Aphids as potential vectors of Plum pox virus: comparison of methods of testing and epidemiological consequences. Acta Horticulturae. 386: 207-18.
25. Lee, Y.; Nelder, J. A.; Pawitan, Y. 2006. Generalized linear models with random effects: unified analysis via H-likelihood. CRC Press. 416 p.
26. Madden, L. V.; Hughes, G.; van den Bosch, F. 2007. The Study of plant disease epidemics. St. Paul. MN USA. ed. 421 p.
27. Parnell, S.; Gottwald, T. R.; Irey, M. S.; Luo, W.; van den Bosch, F. 2011. A stochastic optimization method to estimate the spatial distribution of a pathogen from a sample. Phytopathology. 101: 1184-90.
28. Perry, G. L.; Mille, W. B. P.; Enright, N. J. 2006. A comparison of methods for the statistical analysis of spatial point patterns in plant ecology. Plant Ecology. 187: 59-82.
29. R Core Team. 2014. R: A language and environment for statistical computing. Vienna. Austria. Available in: http://www.R-project.org/
30. Ripley, D. B. 1977. Modeling spatial patterns. J. Royal Stat. Soc. Bulletin. 39: 72-212. 31. Rozas, V.; Camarero, J. 2005. Técnicas de análisis espacial de patrones de puntos aplicadas en ecología forestal. Invest. Agrar: Sist. Recur. Forest. 14: 79-97.
32. Upton, G. J. G.; Fingleton, B. 1985. Spatial data analysis by example. Point Pattern and Quantitative Data. ed. 422 p.
33. Varveri, C. 2006. Epidemiology of Plum pox virus strain M in Greece. Bulletin EPPO. 36: 276-8.
34. Varveri, C.; Dimou, D.; Zintzaras, E.; Di Terlezzi, B. 2001. Monitoring and spatiotemporal analizis PPV-M spread in two apricot orchards in southern Greece. Acta Horticulturae. 550: 129-31.
ACKNOWLEDGEMENTS
This work was supported by INTA. We are grateful to the members of the Statistics and Biometry group of FCA-UNC-CONICET, directed by Dr. M. Balzarini, for their support in statistical analyses.